¿Por qué aprendemos derivadas? Lo que no te dicen en la escuela

Julio Aquino, 16 de Diciembre 2020

A todos nos ha tocado lidiar con las derivadas en algún punto de la universidad o bachillerato, siendo estas una dificultad para muchos, ya que pareciera que estamos resolviendo ejercicios sin parar y cada vez con una complejidad más grande, todo esto sin saber para qué pueden servir verdaderamente.

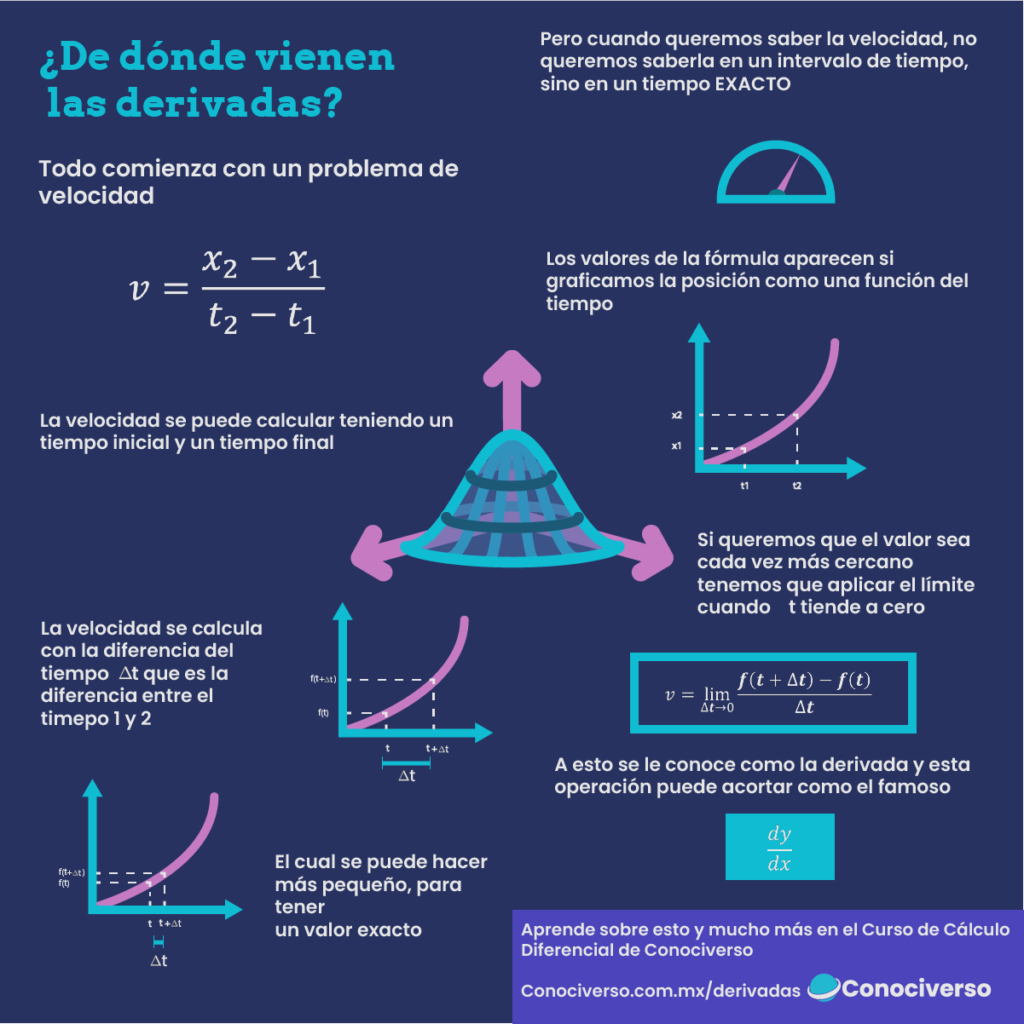
Isaac Newton, uno de los científicos más famosos, tratando de estudiar el movimiento de los objetos, se topó con un dilema que parecía no tener una respuesta aparente. Ya se sabía que la velocidad era definida como el cambio en la posición con respecto al tiempo, podemos comparar esto como el tiempo que toma llegar de un punto A a un punto B, la velocidad la representaríamos como esta distancia dividida entre el tiempo que nos tomó recorrerla.

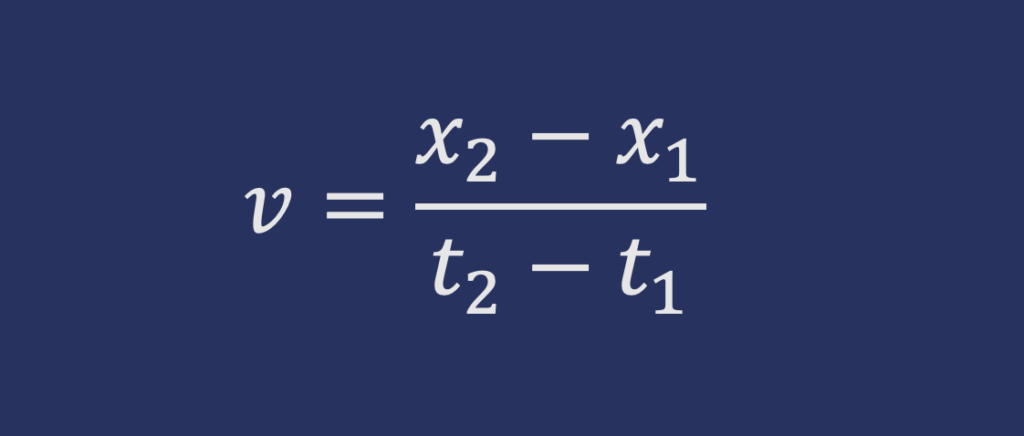
El problema surge cuando queremos saber la distancia en un tiempo exacto, así como en el tablero de un automóvil tenemos nuestra velocidad, no la velocidad que tenemos de un intervalo a otro.

Esta idea pareciera alejarse del concepto de la misma velocidad, ya que para calcularla necesitamos tener un tiempo uno, un tiempo dos, una posición uno y una posición dos. Pareciera entonces que no podemos saber este dato. Isaac Newton y los científicos de la época desarrollaron una forma en la podría conocerse matemáticamente este dato, todo comienza desde analizar la posición de los objetos como una función que depende del tiempo, en la cual podemos encontrar estos valores.

De esta forma podemos considerar que si queremos obtener la velocidad en un punto específico, una manera lógica de lograrlo es haciendo más pequeño el tamaño de delta t, el cual es la diferencia entre el tiempo uno y el tiempo dos, de esta forma cada vez mediríamos la velocidad en un intervalo más pequeño.

Pero nuestra idea no es que el intervalo sea más pequeño, ¡Queremos conocerlo en un punto exacto! entonces podemos pensar que si hacemos que este valor sea infinitamente pequeño podemos hacer que sea más cercano a cero y cuando esto ocurra, no habrá una separación entre el tiempo uno y el tiempo dos.

Esta idea pudo expresarse fácilmente como el límite de la fórmula de la velocidad cuando esta distancia delta t se acerca a cero, y los demás valores los sustituimos con la función evaluada en “t” y “t + delta t”.

De esta forma es como se definió la derivada, esto viene de un problema tan sencillo como el querer calcular la velocidad de un objeto en un tiempo determinado, esta misma ecuación puede expresarse como el famoso dy/dx donde y es cualquier función que dependa de x (que representa cualquier variable).

El cálculo desarrollado gracias a la invención de las derivadas y el Cálculo en general nos pudieron llevar a la luna, sí, A LA LUNA, en Conociverso nos interesa que comprendas mejor cómo surgen los conceptos que nos ayudan a entender el universo, y en el Curso de Cálculo Diferencial puedes aprender mucho más de esto, además de mejorar tus calificaciones, recuerda visitar el curso para que puedas ser parte de este pequeño porcentaje de los que entienden por qué pasan las cosas.